数A割り算の余りの性質 数A合同式modとは 数A合同式modと割り算の余り 数A十の位と一の位の数の求め方;数の性質:第8回 公倍数・最小公倍数の簡単な求め方(3つ以上の数) 100マスのたし算 無料計算プリント;ユークリッドの互除法 ・ユークリッドの互除法とは高校数学A ・ユークリッドの互除法の活用高校数学A 212元1次不定

小学3年の算数の宿題 この解き方なんか変じゃない 夏休み編 掲示板 マイネ王
割り算の余りの性質 a^2019
割り算の余りの性質 a^2019-多項式の割り算では,余りが割る式と同じ次数ではまだ計算の途中とみなす. 余りは必ず割る式よりも次数が低くなっていなければならない. だから,次の割り算のように「係数が分数になっても」余りの次数を下げなければならない. 右の例では,整数係数の多項式を整数係数の多項式で3 割り算の余りの性質 一般に,m を整数とし,2 つの整数a,b をm で割ったときの余りをそれぞれr,r′ とすると,次のことが成り 立つ. 1 ab をm で割った余りはr r′ をm で割った余りに等しい. 2 a b をm で割った余りはr r′ をm で割った余りに等しい.
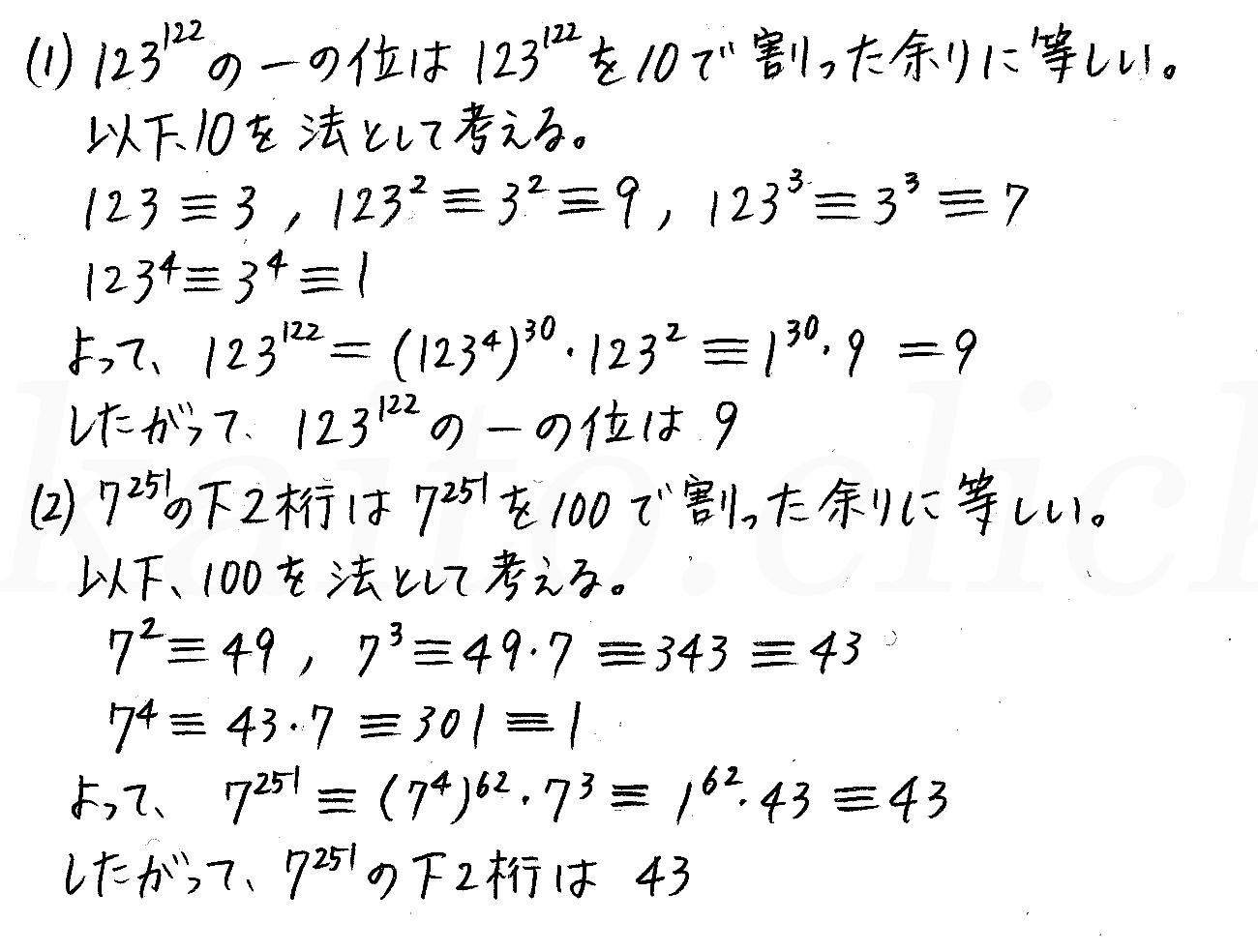



改訂版 4step数学a P160 研究 割り算の余りの性質
香川亮の数学基本大全 整数 数学a43a 割り算の余り(1)余りの性質 整数 ログイン;割り算の商と余り(あまり)を計算します。 割る数、割られる数は共に自然数のみ対応しております。 割られる数 割る数 ÷ = 商: 余り: \) お客様の声 アンケート投稿 よくある質問 リンク方法 余り計算 110 /42件 表示件数 1 1322 歳未満 / 小・中学生 / 非常に役に立った 剰余の定理のおかげで,実際に割り算(多項式の割り算はめんどくさい!)をしなくても P (2) P(2) P (2) を計算するだけで余りが求まりました。 このように 剰余の定理 とは,多項式を (x − a) (xa) (x − a) で割ったときの余りを素早く計算するための定理です。
割り算の余りの性質です (4)です、「6^2」ってどうゆう考えで出てきたんでしょうか? 「6^2」じゃないとダメな理由があるんですか? 時湖 幼頭 11 割り算の人りの性質 次の数を 7 で視った余りを求めよ。 ⑰ 2ナ22 (2⑫ 25 ⑬ の〆の ?王79す3, 2王7の十4 と表して考える基本的な方針で解いてみる数A割り算の余りの性質 コース やる気先生 逆転の数学Ⅰa 高校数学のインプット系講義です。数学Ⅰaの全範囲を網羅しています。初学者にもわかるように丁寧に解説し、中上級レベルの実力が養成できるようになっています。動画だけでも学習可能ですが、準拠教材もあります(講師hpカテゴリー 速さ (2) 割合 (8) 比 (7) 数の性質 (9) 和差算 (4) 仕事算 (5) 濃度 (3) 場合の数 (3) 時計算 (3) 平均算 (3) 規則性 (9) 2進法 (3) 売買
ユークリッドの互除法 ユークリッドの互除法とは高校数学A ユークリッドの互除法の活用高校数学A 212元1次不定方程式 axby=cの整数解(2元1次不定方程式 100マスのわり算 無料計算プリント 余りがない割り算 100ます計算の無料プリント全5種類240回分 目安の時間は? 暗算の計算プリント 整数&小数全25種問無料 メリットやコツも 数の性質:第8回 公倍数・最小公倍数の簡単な求め方(3つ以上の数) 100 この性質は、 大きな数を割った余り を 合同式を利用すると、割り算の余りを求めることができます。 例題② (1) \(16^{100}\) を \(5\) で割った余りを求めよ。 (2) \(2^{50}\) を \(7\) で割った余りを求めよ。 さすがに \(100\) 乗や \(50\) 乗は計算したくありませんね。 合同式のべき乗の性質



67md8co9sqax2m




割り算の余りの性質です Clear
今回の問題は「 除法の性質 」です。 問題 を整数として、 を で割ったときの余りが 、 を で割ったときの余りが のとき、次の値を で割ったときの余りを求めよ。 次のページ「解法のPointと問題解説」 次へ 1 2 整数の分類と証明整数には, 次の基本的な性質があります。 整数全体は, 整数 p (p>0) で割ったときの余り, 0, 1, , p1 によって p 通りに分類できる つまり整数を4で割った余りは0か1か2か3なので, 整数nは必ずこれらの4通りのどれかになります。除法の性質を理解している。 12 末尾に0のある数・÷500の筆算の仕方を考え,末尾に0の 技:末尾に0のある数の除法の簡便 の除法の簡便な筆ある数の除法の簡便な筆算の仕方をまとめる。 な方法による筆算や余りを求め
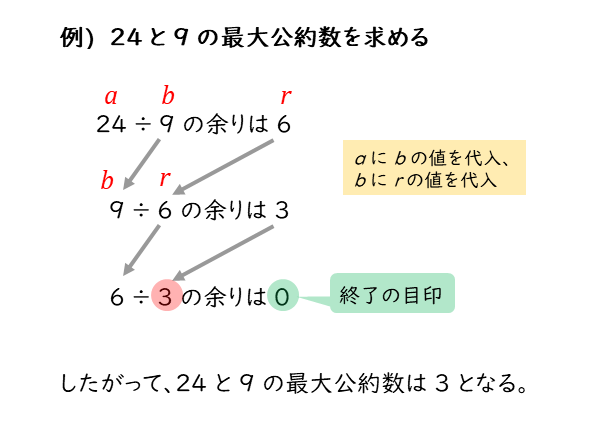



整数の性質 ユークリッドの互除法について 日々是鍛錬 ひびこれたんれん




Python入門 割り算の余りを計算する方法 ポテサラ
その割り算を筆算でやってみることを考えましょ う。その計算が終了するのは,割り算の余りが 0になったときです。もし余りが0でなければ, さらに割り算を続けていくわけですが,余りとし て現れる数は割る数(=分母)未満の数です。整数の性質3 整数の割り算と商および余り 243 (1) 2 ( )(n n n n = 5 4 1 4) 2nが偶数のときn4 は偶数だから( )(n n 1 4)すなわち n n 5 4 は偶数である。 2nが奇数のときn1 は偶数だから( )(n n 1 4)すなわち n n 5 4 は偶数である。 以上より,すべての整数nに対し 2 n n 5 4 は偶数である。 (2第2章で整式の割り算をやりました。その計算は整数の割り算と同じく結構面 倒なものでした。剰余の定理とは,整式をx¡fi のような1次式2 で割ったときの 余りに関する定理です3。この定理は,この場合の余りに限り,簡単に計算する方 法を与えてくれ



48s96ub7b0z5f Net Amari Goudoushiki
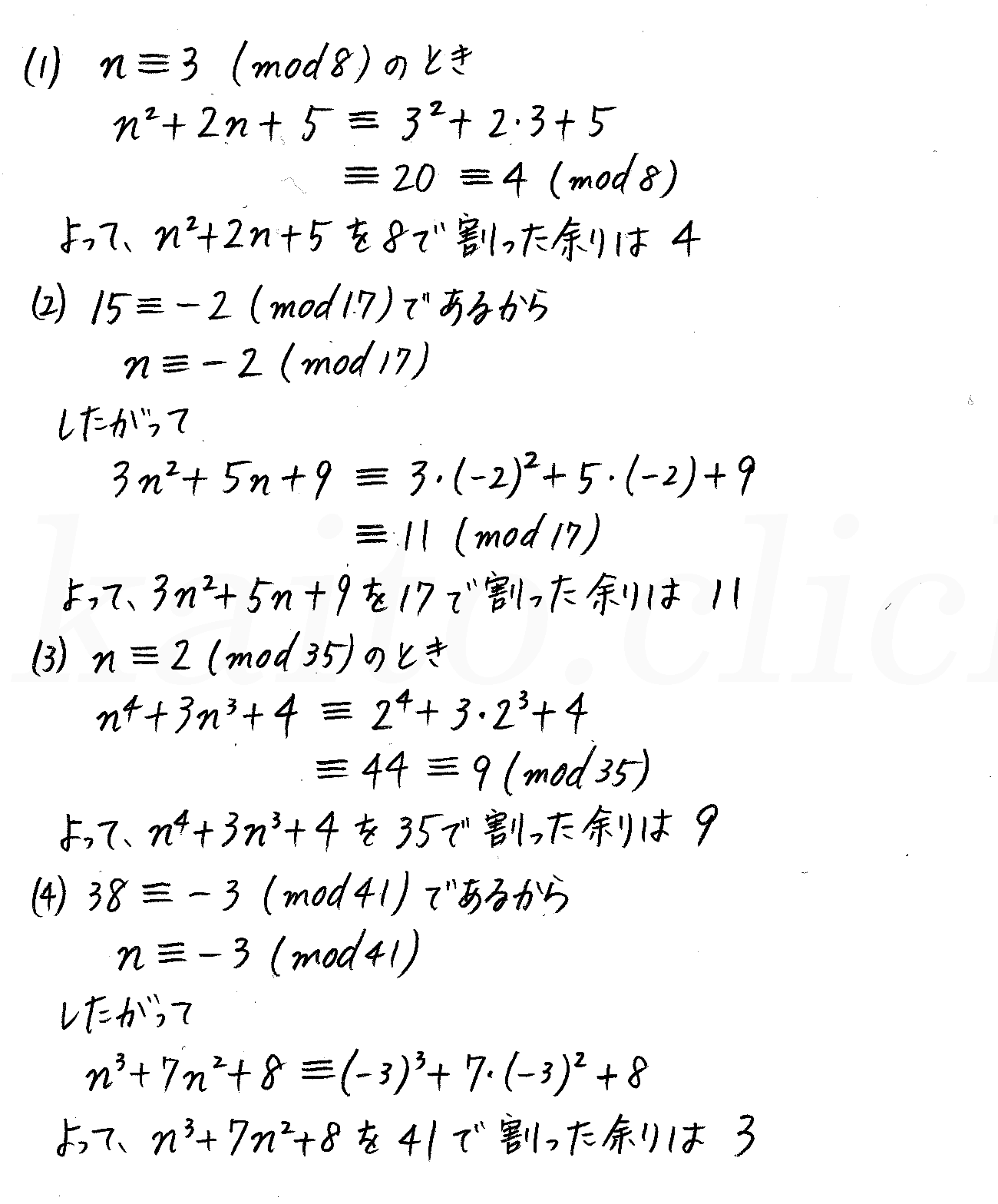



改訂版 4step数学a P160 研究 割り算の余りの性質
・数A割り算の余りの性質 ・数A合同式modとは ・数A合同式modと割り算の余り ・数A十の位と一の位の数の求め方; 割り算の余りの性質です (4)です、「6^2」ってどうゆう考えで出てきたんでしょうか? 「6^2」じゃないとダメな理由があるんですか? 時湖 幼頭 11 割り算の人りの性質 次の数を 7 で視った余りを求めよ。 ⑰ 2ナ22 (2⑫ 25 ⑬ の〆の ?王79す3, 2王7の十4 と表して考える基本的な方針で解いてみるサイトトップに戻る プレミアム会員では、教材がダウンロードでき、快適な動画再生環境が提供されます。 動画再生が完了 この講座を作ってくれた講師の方へ、ボタンを押して感謝の気持ちを伝えましょう




合同式 Mod の意味とよく使う6つの性質 高校数学の美しい物語




D 13 16 1 3 Descubre Como Resolverlo En Qanda
数Aの「割り算のあまりの性質」です。ここの問題の回答なのですが、なぜ「7の2乗」なのですか?「7の3乗」や「7の4乗」ではいけないのですか?回答よろしくお願いします。n 乗の公式は (a b)^n = Σk=0~n{nCk * a^k * b^(n k)・割り算の余りの性質を利用し て,事象を考察しようとして いる。 7 問題演習 5 5 本時の学習 (1) 目標 前回までに学習した,余りによる整数の分類を利用し,様々な問題を解くことで理解を深める。 (2) 展開 過程 学習活動おわりに 広告 ※ お知らせ:名古屋大学21年




式と証明 整式の割り算について 日々是鍛錬 ひびこれたんれん




余りが一致する問題 公務員試験の基礎と競馬のデータ
このトピックでは,整数のかけ算割り算を行います。1 桁のかけ算と割り算から始めて,複数の桁の問題へと進んでいきます。 再編成 (繰り上げ,繰り下げ),余り,そして文章問題をカバーします。 割り算は2種類あるって知っていますか? まとめ 今回はあまり知られていない割り算「 「包含除(ほうがんじょ)」 」について解説しました。 納得しないと先に進めない子にとって、理由の説明もなく「分数の割り算は、逆数をかける」と言われると困ってしまいます。そんな時には「 整数の性質 整数 基本整数の除法と商と余り 18年7月27日 ここでは、整数の除法(割り算)を行ったときの、商と余りについて見ていきます。 目次 正の整数を正の整数で割る;




すうがくぶんか 大人のための高校数学1aでは 三角比の余弦定理や 整数の性質について特に整数のあまりのある割り算や合同式を使った計算の方法などについて解説しました



赤a131b 1 割り算の余りの性質の問題です なぜ赤線部のことはど Yahoo 知恵袋
文字を使う割り算(除法)と余りの問題は、抽象的で苦手な人が多い。そこで、今回の授業では、教科書では説明が省かれているような基本的なテクニックを確認しておこう。 「3で割ると余り1となる数」の表し方 具体的には、問題文の中に 「3で割ると余りが1」 といった表現が出てくること6 割り算の余りの性質 a,b は整数とする。a を6 で割ると2 余り,b を6 で割ると3 余る。このとき,次の式の値を6 で割った ときの余りを求めよ。 (1) a+b (2) ab 整数a と自然数b に対して a=bq+r, 0≦r<b を満たす整数q,r がただ1 通りに決まる。整式の割り算の余りの求め方 「x^100+1をx−1で割った余りを求めよ」とか,「P(x)を(x−2)(xx)がわからなくて割り算ができなかったりするのですが,どうやって余りを求めるのですか? 進研ゼミからの回答! こんにちは。 いただいた質問について,さっそく回答いたします。 質問の確認



Studydoctor 数a 合同式modと割り算の余り Studydoctor




整数の基本性質 数学a フリー教材開発コミュニティ Ftext
小学生の割り算の問題プリントを作りました。 単元・内容ごとに順を追って、または、やりたい内容をピンポイントで選んで、くりかえし練習・学習ができるプリント集です。 小学3年生のわり算 練習問題プリント 小学3年生のわり算筆算 練習問題技2 位数÷1 位数(余りなし) の筆算ができる。 4 2 位数÷1 位数(余りな し)の筆算の仕方を理 解し,その計算ができ る。 ・72÷3の筆算の仕方を考える。 ・72÷3の答えの確かめをする。 ・72÷3の筆算の仕方をまとめる。 ・計算練習をする。算数 割り算ドリルのページへようこそ 上記のボタンから算数割り算ドリル (PDFプリント)がダウンロードできます。 個人利用は無料です (家庭以外での配布は有料です)。 プリント内の数字はランダムです。 大量にありますので、お好きなだけ




中学数学テスト対策 商と余りの関係について Pikuu



あまりが出る小数の割り算の計算手順 小学生に分かりやすく教える方法 数学fun
Degg(x) >degr(x) となる多項式h(x),r(x) がただひと組存在する。 h(x);r(x) をそれぞれf(x) をg(x) で割った商,余りという。 存在と一意性に分けて多項式の割り算に関する基本定理を証明する。 定理(多項式の割算の基本定理) f(x);g(x) は多項式でg(x) は0 多項式でないとする。このとき f(x) =h(x)g(x) r(x);(余りあり) ・余りと除数の大きさの関係 ・答えの確かめ方 ・余りの処理の仕方 1 かけ算 ・乗法の交換法則 4 わり算 ・乗法の意味と商の求め方 ・九九 1回適用の除法計算 (余りなし) 計算 ・倍と除法の意味 3 割り算の筆算(1)




式と証明 整式の割り算について 日々是鍛錬 ひびこれたんれん




高校数学です 4 教えてください Clear
第4講整数の割り算と商・余り(解答) Tweet 基本問題, 定期テスト 3講 最大公約数・最小公倍数の性質(1節 約数と倍数) 問題集3章 整数の性質 1講 ユークリッド互除法(2節 ユークリッド互除法) 問題集3章 整数の性質




4講 整数のわり算と商 余り 1節 約数と倍数 問題集 3章 整数の性質




整数の割り算と商および余り 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開



Studydoctor整数の割り算の商と余り マイナスの割り算も 数a Studydoctor




数aの 割り算のあまりの性質 です ここの問題の回答なのですが な 数学 教えて Goo
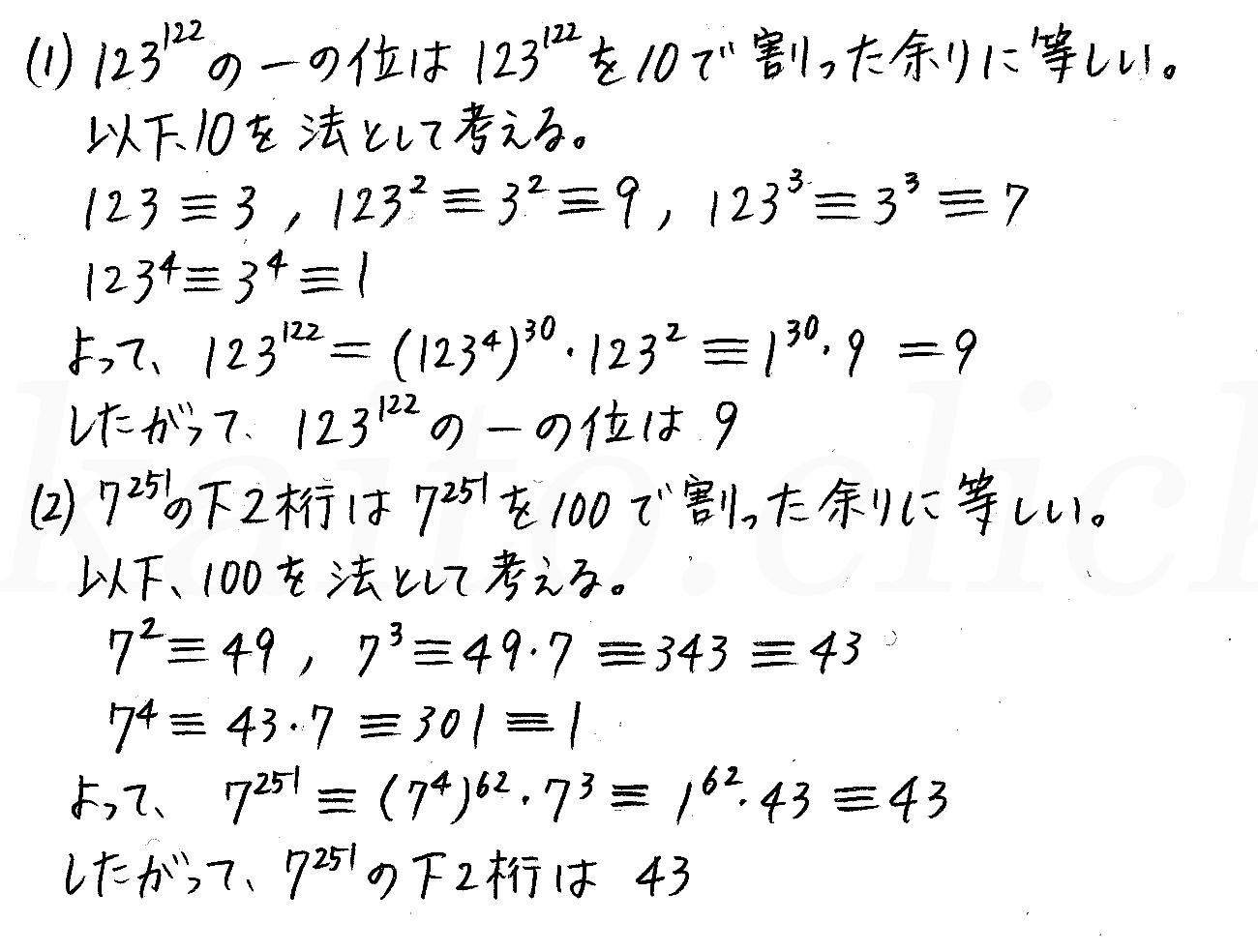



改訂版 4step数学a P160 研究 割り算の余りの性質




60 Off アドバンスノート数学a整数の性質 新課程用 高校数学研究会 啓林館編集部 新興出版社啓林館 単行本 宅配便出荷 新作 Www Teamlabs Es




割り算の余りの性質です Clear




改訂版 4step数学a P157 3 整数の割り算と章および余り




数a 割り算の余りの性質 Youtube



わり算 割り算 の教え方は水道方式でわかりやすく 数学で育ちあう会




基本事項 整数の性質2 割り算の商と余り Youtube




合同式 Mod とは 性質の証明や計算問題の解き方 受験辞典




丸をつけた部分はあまりどうしをかけているのですか Clear




高校数学a 余り を証明する問題1 基本 映像授業のtry It トライイット



48s96ub7b0z5f Net Amari Goudoushiki




高校数学 組立除法による整式の割り算 受験の月




D 13 16 1 3 Descubre Como Resolverlo En Qanda



あまりのあるわり算 説明活動を取り入れた授業 木下幸夫先生 算数3年生の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材



小数点の割り算 筆算のやり方は あまりが出る場合などもイチから解説 数スタ




負の数の割り算と余り 整数と余りの問題 高校数学なんちな




数aのチャートの問題で チャートの解説がいまひとつわかりません もっとわかりやすく教 Clear




競プロ 余りの計算 なかけんの数学ノート



48s96ub7b0z5f Net Amari Bunrui




余り 剰余 の性質をプログラムに活かす Qiita



Studydoctor 数a 割り算の余りの性質 Studydoctor



数学aの割り算のあまりと性質です Aは整数とする Aを7で割ると3 Yahoo 知恵袋



小学4年生の算数 筆算 割り算 割り算の決まり 練習問題プリント ちびむすドリル 小学生



机のしみ New Year Contest 15 L Maspyのhp



割り算のあまりの性質に関する質問です A Nをmで割った余りは R Nをmで割 Yahoo 知恵袋




剰余の定理をわかりやすく証明 二乗で割った余りを求める応用問題アリ 遊ぶ数学



48s96ub7b0z5f Net Amari Goudoushiki




新鮮な多項式 の 除法 最高のカラーリングのアイデア




中学数学2年 文字式の利用 商と余り 受験の月




改訂版 4step数学a P160 研究 割り算の余りの性質




3の100乗を19で割ったあまりは を4通りの方法で計算する Tsujimotterのノートブック




整数の割り算の商と余り マイナスの割り算も 数a Youtube



数学小話 中学校では教えてくれない数の性質 互いに素と余りの関係 日比谷高校のススメ




数の構成 合同式 は割り算と余りの式 大人が学び直す数学




小数点の割り算 筆算のやり方は あまりが出る場合などもイチから解説 数スタ




数a 割り算の余りの性質 Youtube




高校数学 整式を2次式で割ったときの余り 受験の月



数学aの割り算のあまりと性質です Aは整数とする Aを7で割ると3 Yahoo 知恵袋
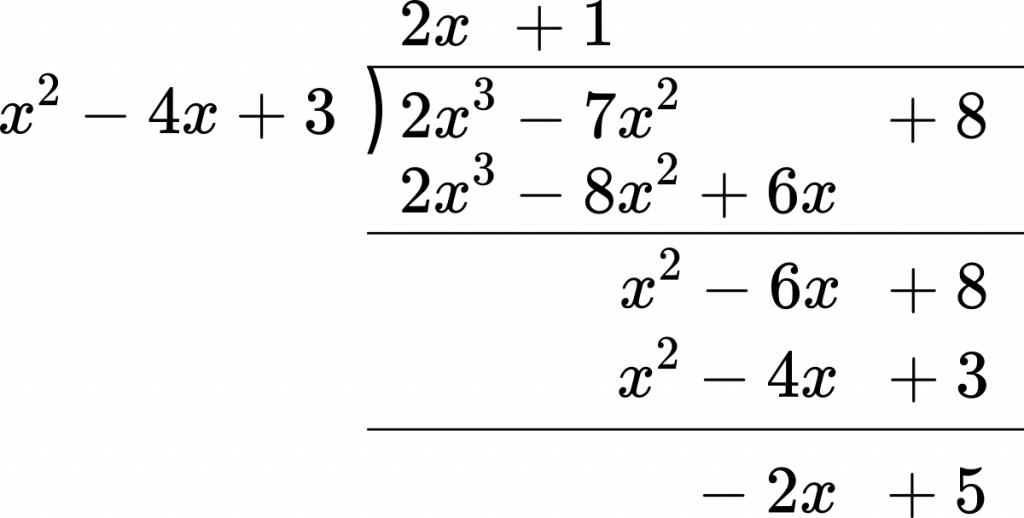



数ii高次方程式 剰余の定理が成り立つ仕組みを掘り下げて考えてみる Mm参考書



48s96ub7b0z5f Net Amari Goudoushiki




あまりが出る小数の割り算の計算手順 小学生に分かりやすく教える方法 数学fun




A B B A 7 3 B 7 4 5 Lihat Cara Penyelesaian Di Qanda




クリアー数学a 数a P144 23 整数の割り算と商 余り




4講 整数のわり算と商 余り 1節 約数と倍数 問題集 3章 整数の性質




小学3年の算数の宿題 この解き方なんか変じゃない 夏休み編 掲示板 マイネ王




メルカリ 数学a 数研出版 参考書 450 中古や未使用のフリマ




暗算の無料プリント 3ケタ 2ケタの整数の割り算 余りなし 全450問 算数パラダイス



高校数学について質問です 今青チャート数a例116の割り算の余りの性質という Yahoo 知恵袋



整数の性質 第5回 整数の割り算と商 余りの授業動画 数学 アオイゼミ



割り算のあまりの性質 算数解法の極意




小4 小数の割り算の筆算のやり方は あまりと答えの小数点は位置が違う 小5 そうちゃ式 分かりやすい図解算数 別館




高校数学a 負の整数の 商と余り 映像授業のtry It トライイット




高校数学a 余り を求める問題1 2数の和 映像授業のtry It トライイット




整数の割り算の商と余り マイナスの割り算も 数a Youtube




世界一早い東大模試解説 2017夏 駿台実戦 文系第一問 オンライン受講 東大に 完全 特化 東大合格 敬天塾



48s96ub7b0z5f Net Amari Goudoushiki



あまりが出る割り算のやり方 大人の学び直し算数 計算のやり方解説 無料




割り算のあまりの性質です これらが成り立つ理由が分かりません Clear




数a 整数 青チャート例題116 4 4 の解説がいまいちよくわからないので Clear
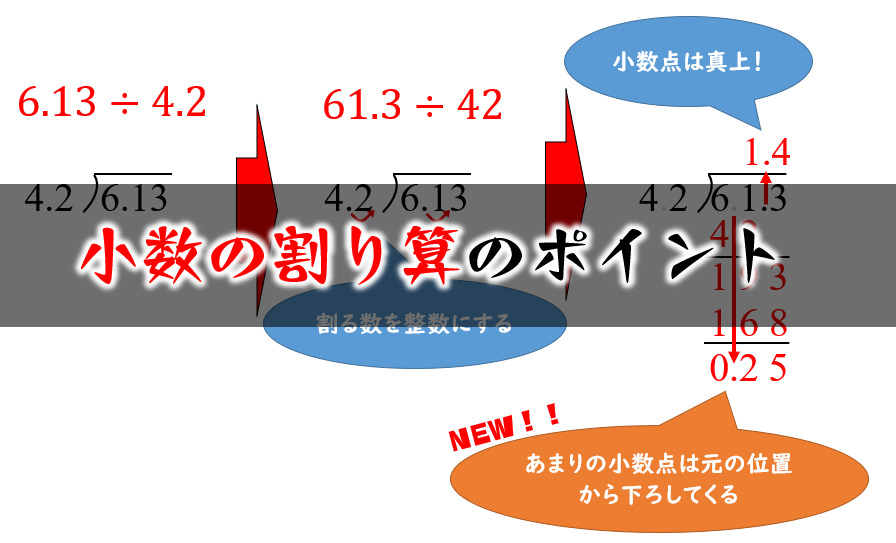



あまりが出る小数の割り算の計算手順 小学生に分かりやすく教える方法 数学fun




N進数変換 2 8 10 16進数の変換方法



高1数学の割り算の余りの性質の問題です 270の 3 の問題の解き Yahoo 知恵袋




合同式 Mod の意味とよく使う6つの性質 高校数学の美しい物語




基本問題 整数の性質2 割り算の商と余り 割り算の余りの性質 No Youtube




高校数学a で割ると余りが を文字で表す 映像授業のtry It トライイット
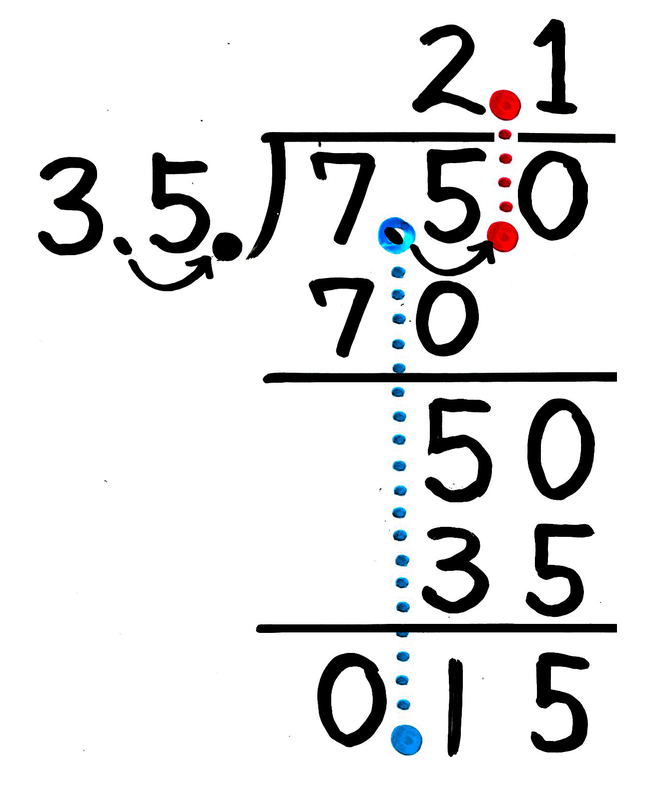



小4 小数の割り算の筆算のやり方は あまりと答えの小数点は位置が違う 小5 そうちゃ式 分かりやすい図解算数 別館




S Live数学館 V Twitter 数研スタンダード数a 3章 整数の性質 29合同式 問題254 255 256 P143 合同式 A B Mod M の仕組みを理解 すると 割り算の余り 商 への理解 が早まります 例題に取り組めば容易に理解できる はずです 食わず嫌いにならないように




高校数学の整数の性質の学び直しで合同式の定義を書き換える 大学受験対策にも タロウ岩井の数学と英語 Note




証明 割り算における商と余り 高校数学 公式の証明 18 Youtube




数学a 整数の性質 整数の割り算と商 余り 4 別解 Youtube



数a 合同式 あまりの性質 青チャートの合同式の性質2と割り算のあま Yahoo 知恵袋




4講 整数のわり算と商 余り 1節 約数と倍数 問題集 3章 整数の性質
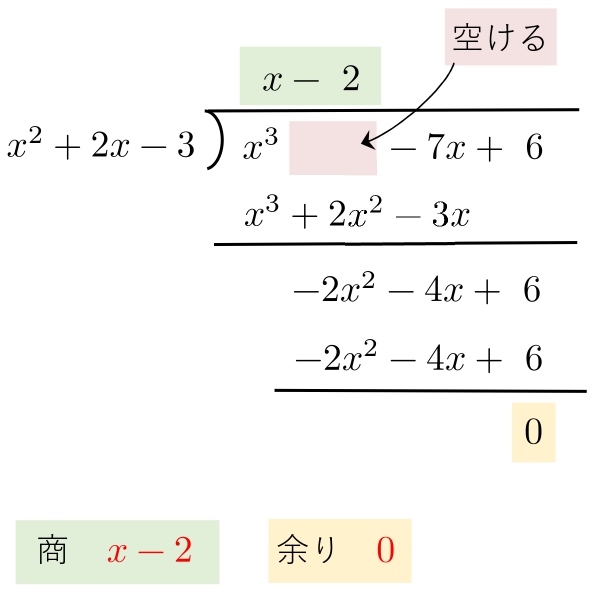



高校数学 整式の除法による余りの求め方 筆算 剰余の定理 組立除法 学校よりわかりやすいサイト



Excel 関数 Mod 関数で割り算の 余り を算出する方法 プログラミングで遊ブログ




例題で学ぶ高校数学 整数の割り算における商と余り




D 13 16 1 3 Descubre Como Resolverlo En Qanda




数ii高次方程式 剰余の定理が成り立つ仕組みを掘り下げて考えてみる Mm参考書




4講 整数のわり算と商 余り 1節 約数と倍数 問題集 3章 整数の性質



0 件のコメント:
コメントを投稿