的應用問題。解應用問題和解一元二次方程式大同小異,比較不同的 是式子必須要自己列出來,那麼怎麼自己列出式子呢? 有四個重要的步驟: 步驟一:理解題目並假設未知數。 步驟二:利用題目裡面所提供的「數量間關係」,列出等式。 步驟三:解一元Title FdData中間期末過去問題中学数学3年(二次方程式応用/係数/数/面積・体積/動点) Author Fd教材開発 Created Date技能:基礎二元一次聯立方程式,數學 > 主題式 > 國中 > 代數與函數 > 直角坐標與二元一次方程式圖形 > 二元一次基測會考歷屆試題。源自於:均一教育平台 願 每個孩子都成為終身學習者,成就自己
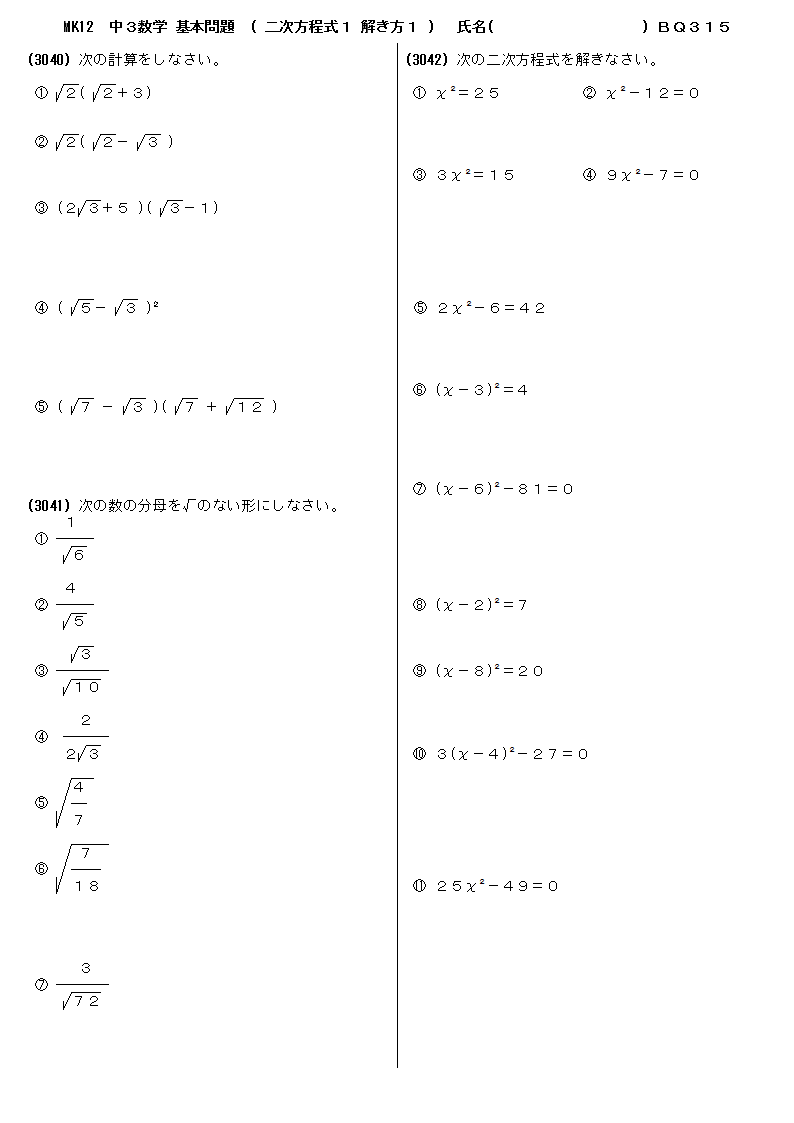
最も人気があります 2 次方程式問題
二次方程式 問題 文章題
二次方程式 問題 文章題-題型 1應用問題 1 兩個正數的差是 5, 它們的乘積是 4 ,求這兩個數。 12 , 17 2 將一個正三角形之一邊長增加 3,另一邊減少 3,第三邊長度不變 ,即成一直角三 角形,求此正三角形之邊長。 12 32次方程式 (x2) (x−2)=2 (3x−2) を解きなさい。 両辺に式があるような二次方程式は,展開・整理して式を左辺に集めてから考えます. 前問と同様に, x=0 を忘れないように気を付けましょう. 方程式 x 2 −2x−35=0 を解きなさい。 左辺が因数分解できる二次
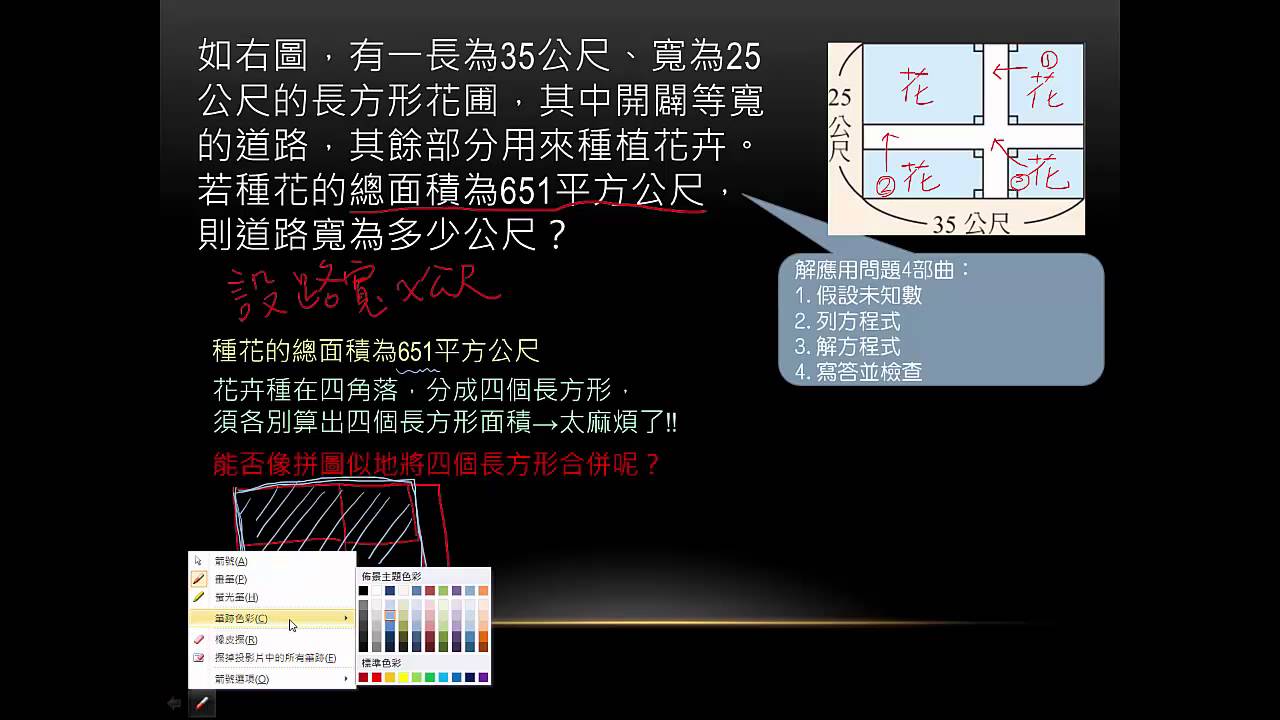



翻轉學習影片 國中 數學 12 2 2 一元二次方程式的應用問題
, where x is the unknown, and a, b, and c are known numbers, with a ≠ 0 The unknowns楊梅國中一元二次方程式應用問題練習 班級:_____ 座號:_____ 姓名:_____ 已知一直角三角形三邊長是連續整數,則此三角形周長為多少?数学33章二次方程式「二次方程式の利用」<応用問題①・解答> 切り取った部分の幅は1㎝ 解説 縦,横ともに両側からχ㎝ずつ切り取られるので, 残った紙の縦の長さは(8-2χ)㎝ 横の長さは(10-2χ)㎝となる。 面積が48㎝2 となるので
今回は、前回より難しい2次方程式の解き方を見ていく このレベルまでできれば、十分ではある。 前回 2次方程式の解き方と練習問題(1)(基) 次回 2次方程式の解き方(3)(難) 31 2次方程式の解き方 311 基本的な2次方程式の解き方(1)(基) 312 2次方程式のの解き方(2)(展開・置き換え・二乗如果我們能夠解一般方程式的根,那麼數字方程式的求根問題當然迎刃而解。 根據 O Neugebauer 的說法,巴比倫人在 1600~1800 BC 已經知道求二次方程式的根。七世紀的印度學者 Brahmagupta(約598~?)寫出方程式 x 2 ax=b 的一個根的公式 。十二世紀的印度學者4 3 一元二次方程式 應用問題 B 9 將一個邊長 公分的正方形,四個角各截去一個等腰三角形後,變成一個正八邊形。 若已假設此正八邊形的邊長為 x公分,則可列成哪一個一元二次方程式?
難関高校の入試問題に挑戦! 今回は、難関高校の入試に出題された二次方程式の難問を解説していきます。 その為、たくさんの問題に触れることで、どの解き方を利用すればいいのかを体感的に身につける必要があります。 今回の記事では、難易度が 2次方程式の文章題の発展問題を扱う。 このあたりは、学校準拠教材や標準レベルの入試問題集ではほとんど練習の機会がない。 前回 ←2次方程式の文章題(1)(代入、数量関係、面積体積)(基~標) 次回 → xの二乗に比例する関数(基) 諸事情でかなり遅れてしまった・・・やっと次回から2次2次方程式 (平方根利用) 基礎 この平方根の考え方を使って2次方程式を解く。 xの2乗が16なので、xは16の平方根になる。 ( )を一つのかたまりと考えて、 (x1)の2乗が6なので、 (x1)は6の平方根になる。 (x5)の2乗が2なので (x5)は2の平方根になる。




世界一わかりやすい数学問題集中3 3章 二次方程式




中学3年生 数学 2次方程式 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
單元五:一元二次方程式的應用問題 71 課文a:一元二次方程式的應用問題 71 2 單元一:一元二次方程式及解的意義 課文:一元二次方程式及解的意義 我們在七上的時候就曾經學過「一元一次方程式」,指的是含有一個未知中学数学 二次方程式の問題 z二次方程式 z二次方程式の解 z二次方程式の解き方(基本) z因数分解を利用した解き方 z平方根を利用した解き方 z二次方程式の解き方(標準) z二次方程式の応用(整数、自然数、図形の面積、容積、動点)13 二元一次方程式應用問題 第一章 二元一次聯立方程式 國中數學第二冊 國一下,內容包含免費的基本觀念教學影片,訂閱課程就可下載「13 二元一次方程式應用問題」的章節講義pdf檔和無限觀看所有精選題型解說影片,皆由名師葛倫親自教學。




世界一わかりやすい数学問題集中3 3章 二次方程式




作業成果 配方法解一元二次方程式 Hahow 好學校
高校数学の基本問題 Gogle site →数ⅠA →数ⅡB →数Ⅲ (旧C) ***最近の更新*** 反復試行の確率(入試問題) 絶対値付き関数の定積分 Rの関数hist () Rの関数sample () 名義尺度データの比率の検定 フィッシャーの正確概要 一般に一変数の三次方程式は = の形で表現される。現代においては、三次方程式の解法といえば、主に代数的解法のことを意味する。 古代バビロニアにおいて既に代数的に解かれていたと考えられている二次方程式と違い、三次方程式が代数的に解かれたのは16世紀になってからで二次方程式の式を変形して A×B=0 という形にできる場合には、因数分解を利用した解き方を使います。 A×B=0 の形で表せる場合 A=0 または B=0 になるという特徴がありましたね。 この特徴を利用して、二次方程式を解いていきます。 詳しくはこちらの




2次方程式の解と係数の決定 無料で使える中学学習プリント




一元二次方程式 應用問題 顧震宇台灣數位學習科技股份有限公司 Ppt Download
資料夾名稱 一元二次方程式 (ch4) 發表人 顧震宇 單位 台灣數位學苑 (k12 數學) 建立 最近修訂公式解一元二次方程式 補充教材 歡迎蒞臨教育部『 國民中學學習資源網 』網站,建議使用Internet Explorer50、Netscape60以上版本,瀏覽器及解析度1024*768展開できる力と、かけて〇、足して の分配法則ができる力が不可欠。 解の公式を使うことができる力も必要です。1か2どちらで行くかを素早く判断できる力も必要。 解が整数の場合は、問題式に当てはめて、サッと確かめをしておくと良い。(なかなか時間がありませんが。)



一元二次方程应用题经典题型汇总 中考数学 中考网




二次方程式
這個六次方程式其實是一個偽裝的二次方程式,即(2)式。 因此我們把三次方程式的求解問題轉化成二次方程式的求解問題。 方程式(3)是怎樣得到的呢? 令 ,, 是方程式(1)的三根, 即 , , 。 方程式(3)的六個根是 。 故得,方程式(3)的六個根是43 一元二次方程式《應用題》 43 應用問題《考古題解》 4T 一元二次方程式《基測經典》 國一下數學實錄 nash;About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators



初中数学知识点总结 二次函数的应用 学习云课堂




2次方程式の応用問題の解き方 文章問題 数学fun
こんにちは、あすなろスタッフのカワイです。 今回は2次方程式の問題演習です。 全部解くことが出来たら、この単元を十分理解していると言っても過言ではありません! では、今回も頑張っていきましょう! あすなろには、毎日たくさ方程式標準問題 1 1 次の方程式を解きなさい。 2x5=9 4x7=1 3x8=5 5x12=3 7x9=19 2x7=13 6x5=13 14x6=15 11=3x4 9=4x7 8=6x1 12=5x2 7=3x13 15=8x11 13=2x35 17=9x19 方程式 (等式の性質を利用)_ 例題と練習 方程式 (移項)_ 例題と練習 方程式 (かっこ、小数11 二元一次方程式《課程實錄》 12 二元一次聯立方程式《課程實錄》 13 二元一次聯立方程式應用題《課程實錄》




09增长率问题一元二次方程初中数学初三 Youtube




一元二次方程式應用問題 例3 Youtube
中学数学標本調査の問題の解き方がわかる3つのステップ 中3数学 二次方程式の利用面積の文章問題の解き方がわかる4ステップ 中1数学 中学数学中央値(メジアン)を求める意味って?このような解き方で、次の問題も考えてみよう。 例題 二次方程式 2(x3) 2 = 10 を解きなさい。 これも先ほどと同じように解くが、前の問題とは違って左辺のかっこの前に係数2がついている。最初にこの係数をとり、前の問題と同じ形にしてから解く。一元二次方程式的問題,就是找拋物線在何處的y 坐標為0,也就是 找拋物線y = ax2 bxc 和x 軸的交點。 3 一元二次方程式的公式解 利用配方法,我們可以得到「一元二次方程式的公式解」,先看一個例子,作法 如下: x2 3x1 = 0) x2 2 3 2 x (3 2)2 = 1 (3 2)2) (x 3 2)2 = 5




0以上2 次方程式問題 シモネタ




数学問題 意外と間違える人が多い二次方程式の基本問題 暇つぶしに動画で脳トレ
練習問題の解答&解説 (1)下の図のように、縦が10m、横16mの長方形の畑がある。 この畑に同じ幅の道を作ったところ、残りの畑の面積が112㎡になった。 この道の幅を求めなさい。 解答はこちら 答え 道の幅を mとするとし、道を端に動かして考えると問題解決の場面で活用できるようにし,方程式をこれまでより多くの場面で問題の解決に活用 できるようにする。 一般の二次方程式を解くのに次の二つの方法がある。 ①因数分解によって一次式の積に変形し,「ab=0 ならば,a=0 または b=0」であることを用 二次方程式の計算問題 それでは、二次方程式を解く練習をしましょう。 平方根の考え方、因数分解、解の公式のどれがいちばん適している問題か考えながら取り組んでみてください。 計算問題①「\((2x − 3)^2 = 7\) を解く」



中3数学 二次方程式の解き方と因数分解 解の公式の覚え方と簡単な計算問題 猫に数学



初中数学知识点总结 一元二次方程的应用 易贤网
第3章 二次方程式 <前: L21 二次方程式の利用(1) の問題 L22 二次方程式の利用(2) の解答 :次> 練習問題1 正方形Aの1辺を2cmずつ長くした正方形Bの面積は121cm 2 になる。 正方形Aの面積を求めなさい。 練習問題2 ある正方形の縦を2cm短く/1/7 2年一次関数総合問題Lv3 5 (2) 点Pはlとx軸の交点 (誤)→点Bはlとx軸の交点 (正) 3年方程式文章題 (割合2)3 (1)解答 2番目の式 yの係数 97 100 (誤)→ 93 100 (正) 7 3年2乗に比例する関数総合問題4 5問題 点A, P, Qを頂点とする (誤)→点D, P, Qを頂点とする二次方程式(にじほうていしき、英 quadratic equation )とは、数学において、二次の多項式関数の零点集合を表す条件のことである。 その零点集合については、特に実数係数であるものについて、幾何学的考察が歴史的に行われ、よく知られている(二元二次方程式については円錐曲線を、一般



一元二次方程配方法 4道提高题 全做对你就是学霸水平 初中 Qq教育网




翻轉學習影片 國中 數學 試題解析 98基測 第二次 第34題 一元二次方程式的應用問題




如何求解四度方程 自然科学21



解一元二次方程及不等式练习题 Doc 沃文网wodocx Com



Http Www2 Chsh Chc Edu Tw Bee 104 a Pdf




年中考数学必考考点 一元二次方程及其应用 初中数学知识点概念大全练习题 哔哩哔哩



求解一元二次方程式不再繁琐 美国数学博士发现简便新方法 罗博




中学数学 二次方程式




一元二次方程式 懶人包



Q Tbn And9gctgoae9bomuk0gymqhrkjzep3izucoijhp9evjmecua8k 13ra4 Usqp Cau
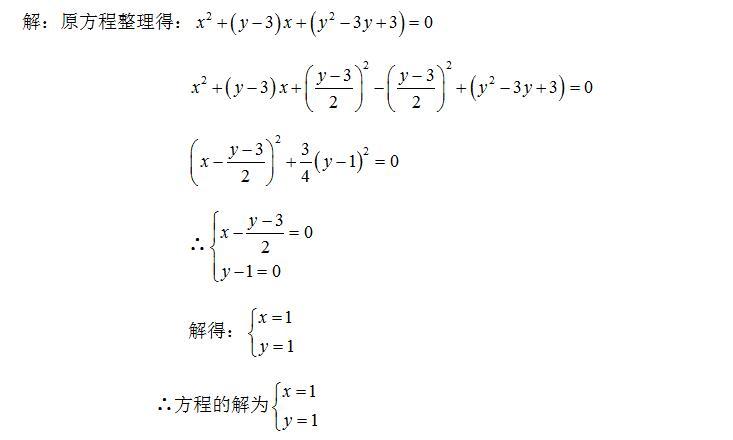



二元二次方程的解法 知乎



中3数学12 二次方程式2 解き方2 基本問題プリント 問題 316




一元二次方程及其应用讲解 初中重点 每日头条




二元二次方程的解法 知乎



高中常见题 解三元二次方程组 哔哩哔哩 つロ干杯 Bilibili




二次方程式の解がわかっている問題は xに代入して計算しよう 中学や高校の数学の計算問題



韦达定理 一元二次方程根与系数的关系 科普中国



一元二次方程练习题精选一 初三数学 中考网




最も欲しかった 数学2 次方程式 ニスヌーピー壁紙



1
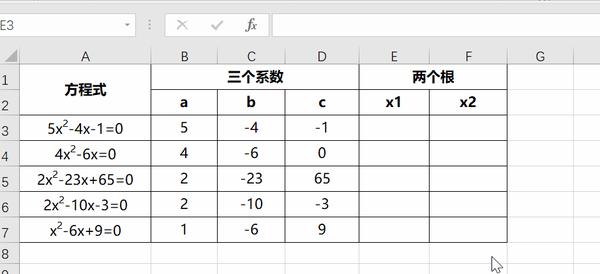



Excel求解多元一次 一元二次方程组就是这么简单 知乎
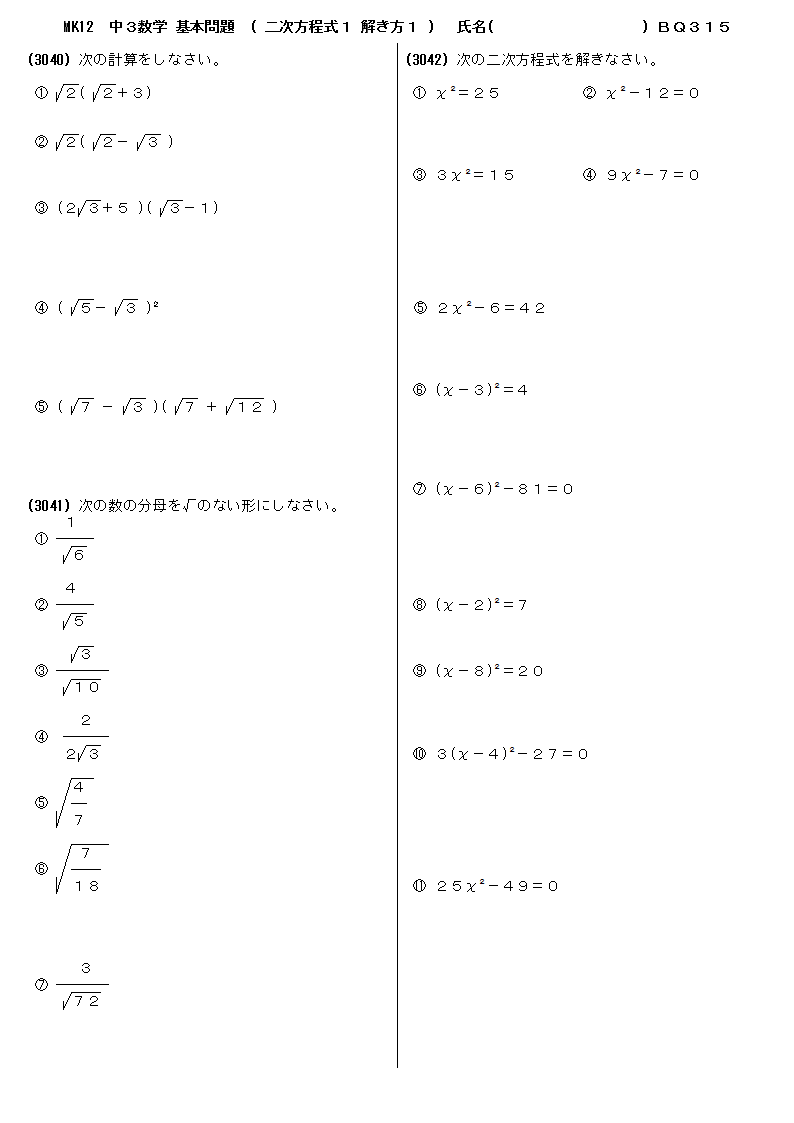



最も人気があります 2 次方程式問題
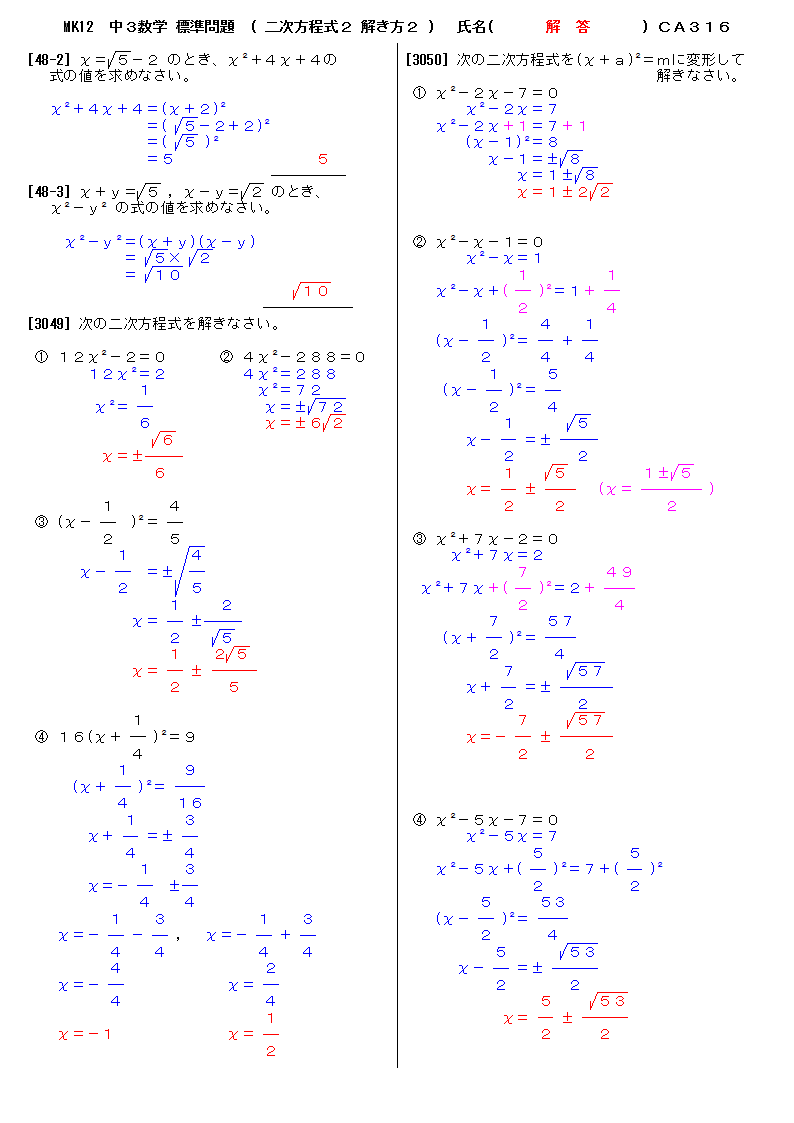



無料 中3数学 標準問題 解答プリント 316 2次方程式2 解き方2




中学3年生 数学 2次方程式 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



初中数学知识点总结 一元二次方程的应用 学习云课堂




109 數學基礎自學講義八年級 一元二次方程式的應用問題 第三冊4 3 Shareclass




解一元二次方程十字相乘法专项练习题 知乎
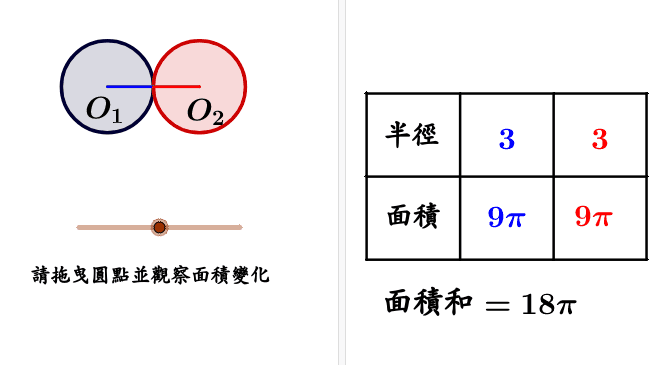



一元二次方程式 應用問題 兩圓相切 3 Geogebra
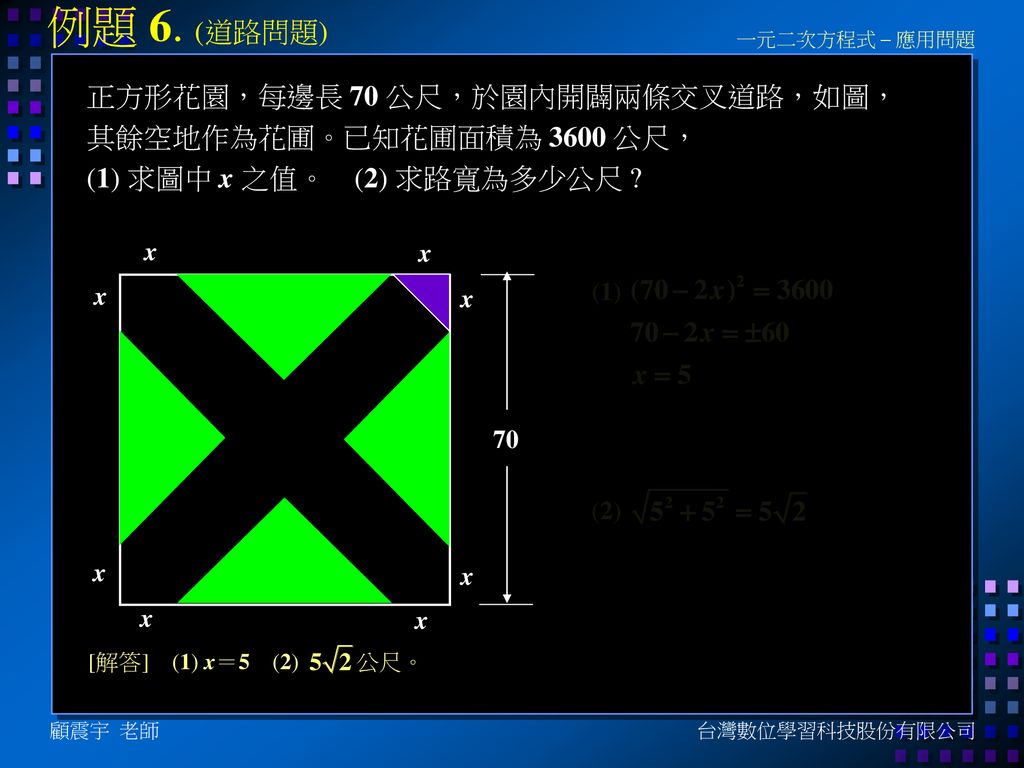



一元二次方程式 應用問題 顧震宇台灣數位學習科技股份有限公司 Ppt Download




亿源老师教案发表 配方法解一元二次方程式 备课吧




北师大版九年级数学上思维特训 七 含答案 一元二次方程根与系数关系的运用技巧 七七文库www 77wenku Com




解一元二次方程式 明誠中學程式設計學習網




2次方程式の文章題ー図形の問題 無料で使える中学学習プリント




基測數學 90v2 單選19 一元二次方程式的應用問題 評量專區 均一教育平台




一元二次方程应用题总结分类及经典例题 每日头条




有人會嗎一元二次方程式的應用問題 Clear




中学3年生 数学 2次方程式 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




翻轉學習影片 國中 數學 12 2 2 一元二次方程式的應用問題




1 次方程式文章題 ニスヌーピー壁紙



綜 一元二次方程式應用問題 考題 台灣數位學苑 K12 數學
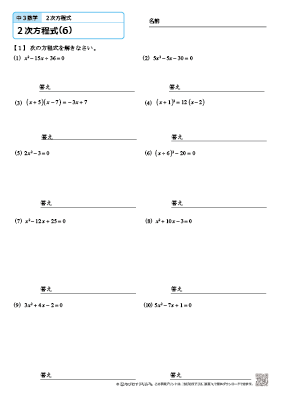



中学3年生 数学 2次方程式 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




巧用十字相乘法解一元二次方程 图文解释 百度经验




翻轉學習影片 國中 數學 一元二次方程式 一元二次方程式應用問題 練習2



問題 數學問題一元二次方程式 校園生活哈啦板 巴哈姆特




这几类一元二次方程应用题不会 中考考高分难了 热点题 楠木轩



2次方程式とは 1分でわかる意味 解き方 解の公式 因数分解との関係



一元二次方程应用题 弄明白握手问题 只需5分钟 比赛



Q Tbn And9gcrwr5k W1f2iibd39mbbjyhda5ozoo5bwykspo4weqwhlvaeg X Usqp Cau




第3章 方程式



康軒國中fun學練功坊數學14一元二次方程式 蝦皮購物




一元五次方程无求根公式的直观解释




0以上2 次方程式問題 シモネタ




二次方程式の利用 チーム エン



名師課輔網 數學一元二次方程式的應用




怎么画一元二次方程的函数图像x X 2 0 顶点坐标是不是 1 2 雨露学习互助




中学3年生 数学 2次方程式の活用 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中考数学 一元二次方程的根与系数的关系与代数式的恒等变形 每日头条



一元二次方程考点透视 第52周 综合复习 初中人教五四制 数学中国网



解一元二次方程及不等式练习题 Doc 沃文网wodocx Com




二次方程式の利用の問題の解き方 カレンダー 現役塾講師のわかりやすい中学数学の解き方




高校数学 文字係数の2次方程式 Ax Bx C 0 受験の月



一元二次方程的应用题 十五种必考题型总结
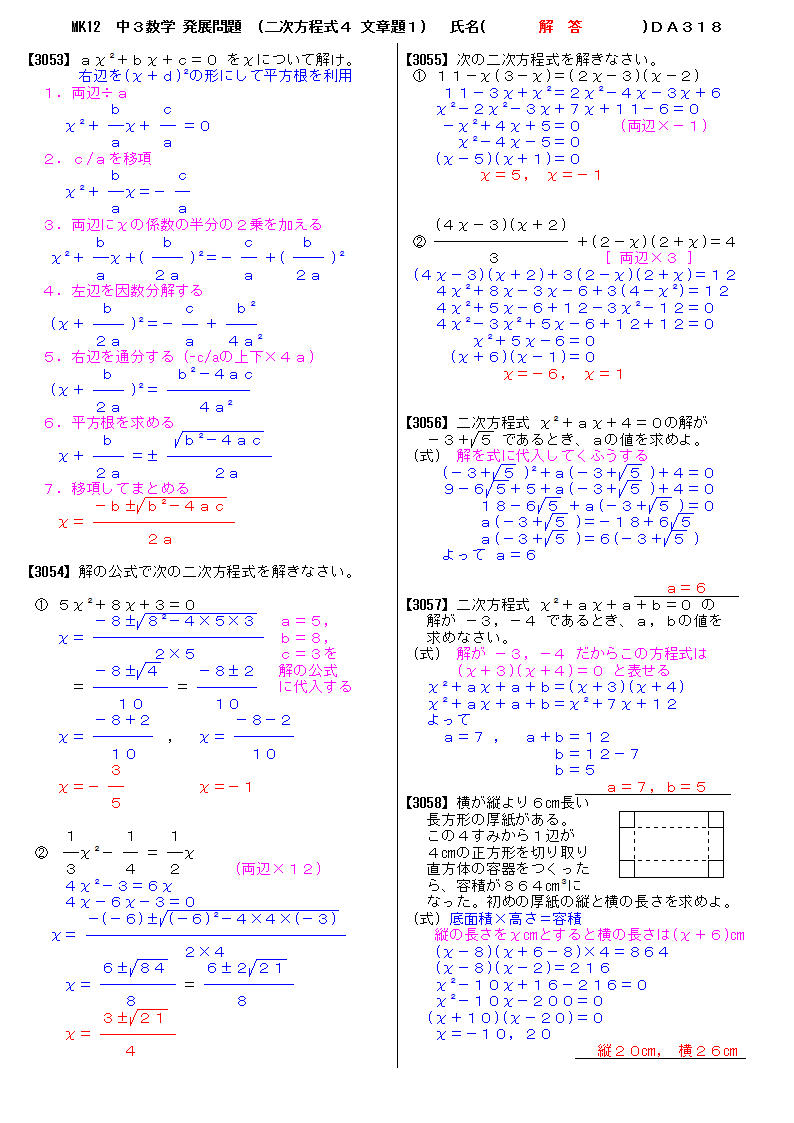



無料 中3数学 発展 応用問題 解答プリント 318 2次方程式4 文章問題1




十字交乘part Vscizr




中3 中3数学 2次方程式 中学生 数学のノート Clear



Q Tbn And9gcskwhhvvfmhhhoiqlmko5jaa7cw6bcheq Snuulphiez3ruztc6 Usqp Cau




一元二次方程式應用問題 例7 8 已下架內容 均一教育平台




2次方程式ーいろいろな計算 無料で使える中学学習プリント




翻轉學習影片 國中 數學 12 2 2 一元二次方程式的應用問題




二次方程式で解の公式を使う問題 見分け方は因数分解がポイント 中学や高校の数学の計算問題



一元二次方程的应用题 十五种必考题型总结



23 2 一元二次方程的解法 5 修订版教案 Rar 华九上 22 2一元二次方程 的解法 初中华师大版13版 数学中国网 Mathschina Com



21 6 1 二元二次方程组的解法 哔哩哔哩 Bilibili




一元二次方程式 黃金比例之絕妙速解 Youtube




整数解をもつ連立3元2次方程式を解こう 2017年度前期日程の一橋大学入試問題 身勝手な主張




愛學網播放影片




三元二次方程 三元二次方程是指有三個未知數 最高次數為二次的方程 一般 百科知識中文網




二次方程式の解き方のまとめ 中学生に覚えてほしいパターンは5つ 中学や高校の数学の計算問題
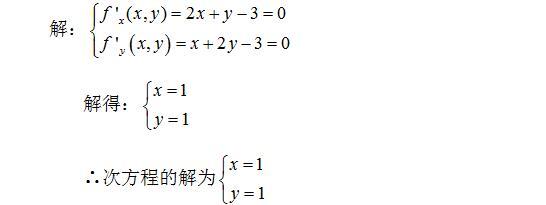



二元二次方程的解法 知乎




109 數學基礎自學講義八年級 一元二次方程式的應用問題 第三冊4 3 Shareclass




一元二次方程的虚数根 一元二次方程的虚根怎么算 三人行教育网 Www 3rxing Org




例題 利用配方法解一元二次方程式2 二次項係數不為1 數學 均一教育平台




一元二次方程的實際應用 常見應用題的解題方法及步驟 每日頭條
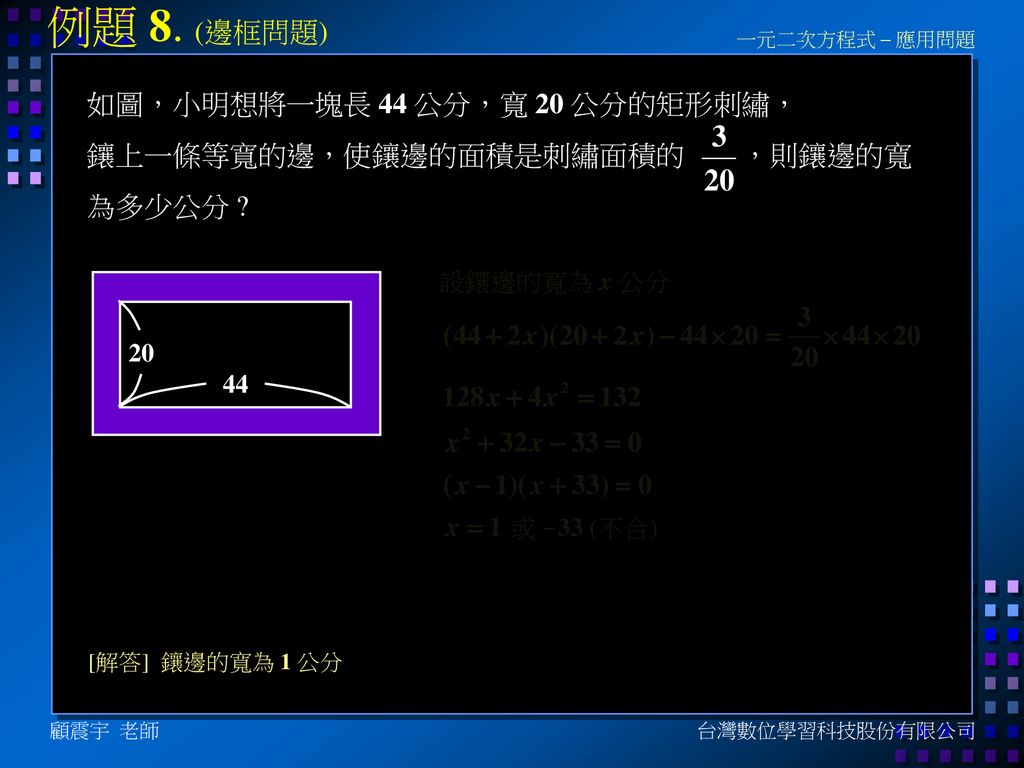



一元二次方程式 應用問題 顧震宇台灣數位學習科技股份有限公司 Ppt Download




初中数学一元二次方程求根公式 一元二次方程的解法 一元二次方程根与系数的关系 101教育知识点频道手机端
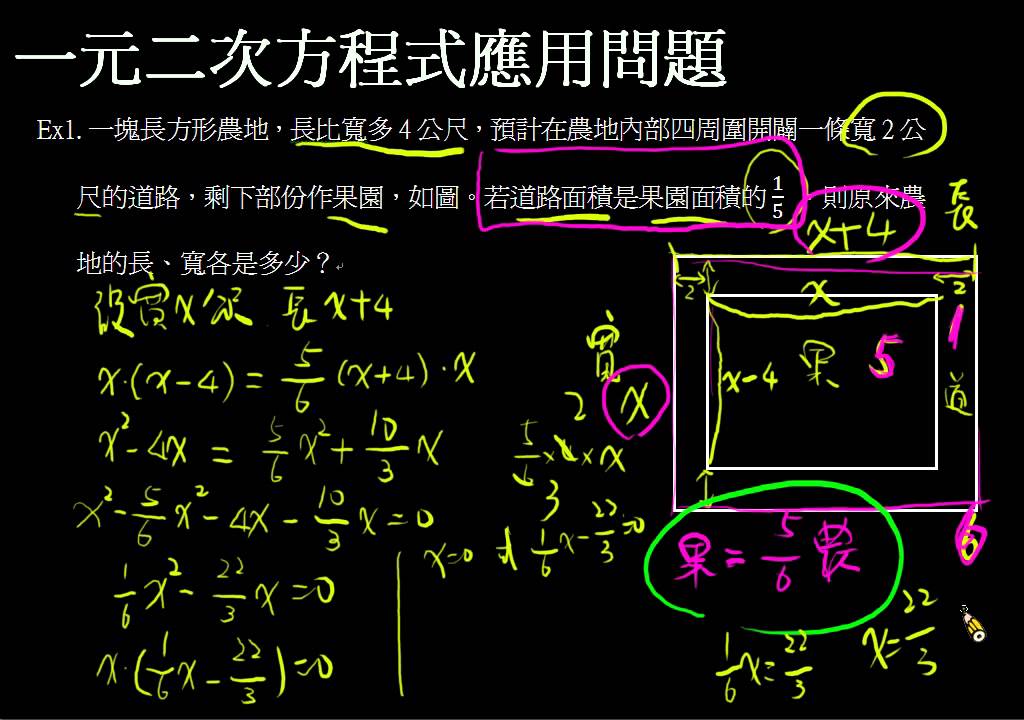



一元二次方程式應用問題 例1 2 Youtube




0以上2 次方程式問題 シモネタ




中学3年数学 二次方程式 解の公式 確認問題2 あんのん塾



0 件のコメント:
コメントを投稿